Data Structures and Algorithms - Performance Analysis of Algorithms and Recurrences
- Option : D
- Explanation : Suppose a list contains n elements, consider first three element and find middle element which will be neither maximum nor minimum. Hence it is θ(1).
- Option : C
- Explanation : I or III or IV but not II
as
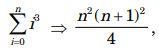 this can be represent by Θ(n4, O(n5), Ω(n3) but not Θ(n5)
this can be represent by Θ(n4, O(n5), Ω(n3) but not Θ(n5)
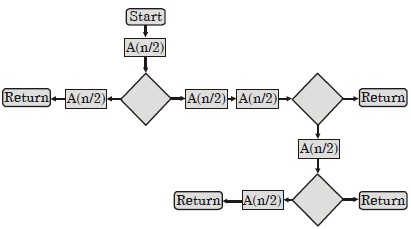
- Option : A
- Explanation : The worst case recurrence reaction for flow chart is T(n) = 5 T(n/2)+ 1 Apply master’s method n log25 ⇒ n2.32 > 1 T(n) = O(n2.32) So, α = 2.32
- Option : C
- Explanation : Delete operation require O(1) time total O(N) Delete so time is = O(n). Insert require O(n) time in worst case total O (logn) insert so time is = O(Nlogn) to Search (logn) key time is = nlogn. To perform decrease key we need O (n) time (because after decrease we need to arrange elements in sorted sequerce) so total O(N) decrease key So total time is O(N2) All operations put together than worst time is O(N2)


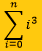 and the
following choices for X
I. θ(n4)
II. θ(n5)
III. O(n5)
IV. Ω(n3)
The equality above remains correct if X is
replace by
and the
following choices for X
I. θ(n4)
II. θ(n5)
III. O(n5)
IV. Ω(n3)
The equality above remains correct if X is
replace by