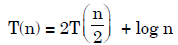Data Structures and Algorithms MCQ - Performance Analysis of Algorithms and Recurrences

66 Which one of the following correctly determines the solution of the recurrence relation with T(1)= 1?

Since f(n) = log n
a = 2, b = 2
finding log_ba using master’s method = log₂2 = 1
Hence, f(n) = n'
So, T(n) = Θ(n)

67 Suppose we have a balanced binary search tree T holding n-numbers. We are given two numbers L and H and wish to sum up all the numbers in T that lie between L and H. Suppose there are m such numbers in T.
If the tightest upper bound on the time to compute the sum is O(n^a log^bn + m^c log^dn), the value of α + 10b + 100c + 1000d is ____.

Note: Numerical type question

The time complexity is O (m + logn)
So C = 1, d = 0, a = 0, b = 1
0 + 10 × 1 + 100 × 1 + 1000 × 0 = [110]

68 Consider the following C function.

int fun 1 (int n)

{ int i, j, k, p, q = 0;
for (i = 1; i<n; ++i)
{ P = 0;
for(j = n; j > 1; j = j/2)
++p;
for (k=l; k<p; k=k*2)
++q;
} return q;
}
Which one of the following most closely approximates the return value of the function fun1?

* Outer loop (for i) executed n times.
* Loop (for j) executed logn times so value of p = logn.
loop (for k) executed log p times.
So value of q = log p = log logn.
for every value of i loop (k) is executed so return value is n * log logn

69 An algorithm performs (logN)^1/2 find operations, N insert operations, (logN)^1/2 delete operations, and (logN)^1/2 decrease-key operations on a set of data items with keys drawn from a linearly ordered set. For a delete operation, a pointer is provided to the record that must be deleted. For the decrease-key operation, a pointer is provided to the record that has its key decreased. Which one of the following data structures is the most suited for the algorithm to use, if the goal is to achieve the best total asymptotic complexity considering all the operations?

Unsorted array
The algorithm perform
find operation (log N)^½
Insert operation N
delete operation (log N)^½
decrease key operations (log N)^½
Hence unsorted array is best data structure for all above operations.

70 Consider a complete binary tree where the left and the right subtrees of the root are maxheaps. The lower bound for the number of operations to convert the tree to a heap is

The subtrees are already Max-heap, so to make it half, we have to heap if the root, which takes Ω(log n) time.