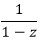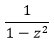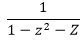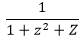Data Structures and Algorithms - Performance Analysis of Algorithms and Recurrences
27. What is the generating function G(z) for the sequence of Fibonacci numbers?
- Option : C
- Explanation : Assuming Fibonacci Sequence as :- 1, 1, 2, 3, 5, 8, 13, ......
So, sequence an = 1,1,2,3,5,8,13,… where, n=0,1,2,3,…
Now, The Generating Function for the sequence an of real numbers is defined as:
So, For the given Fibonacci Series :-
⇒ G(z) = 1+z+2z2+3z3+5z4+8z5+13z6+...+fnzn+... →(1)
Now , Shift one position right and multiply by 'z' :-
⇒ zG(z) = z+z2+2z3+3z4+5z5+8z6+... →(2)
Now, Shift one more position right and multiply by 'z' :-
⇒ z2G(z)=z2+z3+2z4+3z5+5z6+8z7+... →(3)
Now, Add Equation(2) and Equation(3) :-
⇒ zG(z)+z2G(z)=z+2z2+3z3+5z4+8z5+13z6+...
⇒ zG(z)+z2G(z)=G(z)−1 (From(1))
⇒ G(z)−zG(z)−z2G(z)=1
⇒
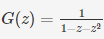So,Generating Function for the given Fibonacci Series is:−
28. Which of the following is false?
- Option : B
- Explanation : (A)
Here 100 is constant so we can say both function are equal .
Hence it is true.
(B) √(logn) = O(log logn)
growth rate of √(logn) is greater then loglogn so it is false.
(C) If 0 < x < y then nx = O(ny) is always true.
(D) 2n ≠O(nk)
if k is constant then this statement is false but here nothing is mentioned about K.
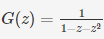
- Option : C
- Explanation :
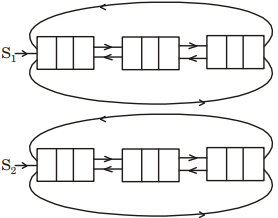Algo for concatenation is ⇒
{
t1 = S1 → nxt ;
t2 = S2 → nxt ;
t1 → nxt = S2
t2 → nxt = S1
S1 → nxt = t2
S2 → nxt = t1
}
it is sequential alqoni them so complexity is O(1)
- Option : B
- Explanation : f(n) = n2 logn g(n) = n (logn)10 Here we can remove common factor from both the function to simply the value of f(n) & g(n) So f(n) = n g(n) = (logn)9 Now choose the largest value of n to compare both the function. if n = 2100 then f(n) = 2100 g(n) = (100)9 f(n) > g(n).
