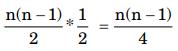Data Structures and Algorithms - Performance Analysis of Algorithms and Recurrences
- Option : A
- Explanation : 20, 24, 30, 35, 50
Step 1 : We take
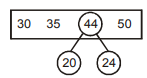 Comparisons = (20 + 24 – 1) Max = 43
Step 2 :
Comparisons = (20 + 24 – 1) Max = 43
Step 2 :
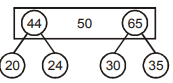 Total comparison = 43 + (65 – 44) = 64
Step 3 :
Total comparison = 43 + (65 – 44) = 64
Step 3 :
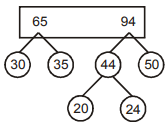 Total comparison = 64 + 19 = 83
Step 4 :
Total comparison = 64 + 19 = 83
Step 4 :
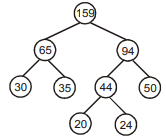 Total comparison = 93 + 65 = 158
= 158 + 93 + 64 + 43 = 358
Total comparison = 93 + 65 = 158
= 158 + 93 + 64 + 43 = 358
92. Give the correct matching for the following pairs:
| List-I | List-II | ||
| A. | O(logn) | P. | Selection |
| B. | O(n) | Q. | Insertion sort |
| C. | O(n log n) | R. | Binary search |
| D. | O(n2) | S. | Merge sort |
Codes:
(a) A – R B – P C – Q D – S
(b) A – R B – P C – S D – Q
(c) A – P B – R C – S D – Q
(d) A – P B – S C – R D – Q
- Option : D
- Explanation : Selection sort = O (n2) Insertion sort = O (n2) or (O(n) in best case) Binary Search = O (logn) Merge Sort = O (n logn) None of the options is true
94. If T1 = O(1), give the correct matching for the following pairs:

- Option : D
- Explanation : T(n) = T(n–1)+n ⇒ O(n2) T(n) = T(n/2) + n ⇒ O(n) T(n) = T(n/2) + n logn ⇒ O(n logn) T(n) = T(n–1) + logn ⇒ O(log2n)