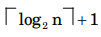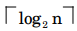Data Structures and Algorithms - Performance Analysis of Algorithms and Recurrences
- Option : B
- Explanation : Here foo(1) is recursive function. Spare complexity is O (n) as there can be at most O (n) active function at a time
- Option : B
- Explanation : Space complexity is O (n). The space we need array of size O (n). The space required for recursive call would be O (1) as the value would be taken from array again & again
- Option : B
- Explanation : T(n) = 2T(√n) + 1 Put n = 2k T(2k) = 2T(nk/2) + 1 replace T(2k) by S(k) S(k) = 2 S(k/2) + 1 Apply masters Klog22 ⇒ k > 1 So Θ(k) Now we know n = 2k, k = log2(n) then Θ(logn)
- Option : D
- Explanation : Since, j increases in power of 2's.
if statement j = j * 2 executes k times, then
2k < n
⇒ k < log2 n
Since k will be integer,
total number of comparison
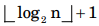 (when loop exits)
(when loop exits)


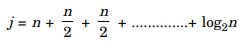 term
If n is not a power of 2, then there will be minor differences of 1 at
term
If n is not a power of 2, then there will be minor differences of 1 at 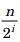 wherever
wherever 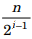 is odd.
Hence val(j) computed on the basis of n = 2n will give a fair answer
is odd.
Hence val(j) computed on the basis of n = 2n will give a fair answer
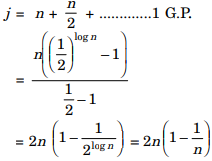 = 2(n – 1) = θ(n)
= 2(n – 1) = θ(n)