Computer System Architecture - Memory Hierarchy
- Option : A
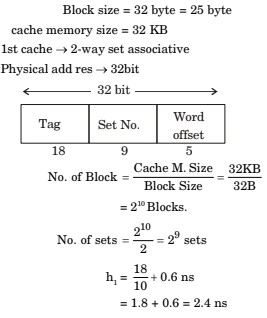
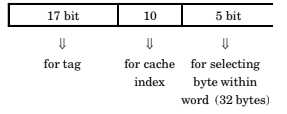
- Explanation : Here, we have 32 bit virtual address space.
32 kB cache memory hence, we need 15 bit for occuring them (not all for indexing explained next). So 17 used for tag.
But here cache are in block of 32 bytes. So, there actually 1 K (blocks) for a indexing 1 K location, we need 10 bits.
Remainder five are used for selecting byte
| Capacity | Mapping method | Block size | |
| 1-cache | 4K words | Direct mapping | 4 Words |
| D-cache | 4K words | 2-way set associative mapping | 4 Words |
| 1, 2-cache | 64K words | 2-way set- associative mapping | 16 Words |
Capacity Mapping method Block size 1-cache 4K words Direct mapping 4 Words D-cache 4K words 2-way set-associative mapping 4 Words L2 cache 64K words 4-way set-association mapping 16 Words The length of the physical address of a word in the main memory is 30 bits. The capacity of the tag memory in the 1-cache D-cache and L2-cache is, respectively,
- Option : A
- Explanation : 1. I-cache
Number of blocks in cache = 4K/4 = 210 blocks.
Bits to represent blocks = 10
Number of words in a block = 4 = 22 words.
Bits to represent words = 2.
tag bits = 30 – (10 + 2) = 18.
Each block will have it's own tag bits.
So total tag bits =1K * 18 bits.
2. D-cache
Number of blocks in cache = 4K/4 = 210 blocks.
Number of sets in cache = 210/2 = 29 sets.
Bits to represent sets = 9.
Number of words in a block = 4 = 22 words.
Bits to represent words = 2
tag bits = 30 – (9 + 2) = 19
Each block will have it's own tag bits.
So total tag bits = 1K * 19 bits.
3. L2 cache
Number of blocks in cache = 64K/16 = 212 blocks.
Number of sets in cache = 212/4 = 1024 sets.
Bits to represent sets = 10
Number of words in cache = 16 = 24 words.
Bits to represent words = 4.
tag bits = 30 – (10 + 4) = 16
Each block will have it's own tag bits.
So total tag bits = 212 * 16-bits = 4K * 16-bits.
Consider two cache organizations : The first one is 32 KB 2-way set associative with 32-byte block size. The second one is of the same size but direct mapped. The size of an address is 32 bits in both cases. A 2-to-1 multiplexer has latency of 0.6 ns while a k-bit comparator has a latency of k/10 ns. The hit latency of the set associative organization is h1 while that of the direct mapped one is h2
Consider two cache organizations : The first one is 32 KB 2-way set associative with 32-byte block size. The second one is of the same size but direct mapped. The size of an address is 32 bits in both cases. A 2-to-1 multiplexer has latency of 0.6 ns while a k-bit comparator has a latency of k/10 ns. The hit latency of the set associative organization is h1 while that of the direct mapped one is h2
- Option : B
- Explanation : For identifying each of 128 lines uniquely,
number of bits required = 7 bits.
Since each line is of size 64 words, so number of bits needed to identify each word uniquely = 6 bits. Now, since there are 20 bits in address generated by CPU
Bits needed for tag = 20 – (7 + 6) = 7 bits.