PREVIOUS YEAR SOLVED PAPERS - GATE 2019
16. Which one of the following is NOT a valid identity?
- Option : B
- Explanation : (a) x ⊕ y = (xy + x′y ′)′ = (xy )′ = x ⊕ y, it is valid. (b) (x + y) ⊕ z = (x + y).z + (x + y)z = xyz + xz + yz = 1 4,6 2,6 = Σm(1, 2, 4, 6) (x + y) ⊕ z = x(y+z) + x (y+z) = xy + xz + yz = 2,3 1,3 4 = Σm(1, 2, 3, 4) (x + y) ⊕ z ≠ x ⊕ (y + z) So option (b) is invalid. (c) (x ⊕ y) ⊕ z = x ⊕ (y ⊕ z) Associativity is true on Ex-OR operator so it valid. (d) x ⊕ y = (x + y)(x + (y) = (x + y)xy = (x + y)x0 = (x + y), so it is valid.
17. If 𝐿 is a regular language over Σ = {𝑎,}, which one of the following languages is NOT regular?
- Option : B
- Explanation : If L is regular, L.LR is also regular by closure property. Suffix (L) and Prefix (L) are also regular by closure property. However option (b) {wwR |w∈L} need not be regular since if L is an infinite regular language, then {wwR |w ∈ L} will not only be infinite, but also non-regular. Since it involves string matching and we can increase in length indefinitely and then finite automata FA will run out of memory.
- Option : B
- Explanation : Given R1 is a equivalence relation, because it satisfied reflexive, symmetric, and transitive conditions:
- Reflexive: a = g–1ag can be satisfied by putting g = e, identity “e” always exists in a group.
- Symmetric:aRb ⇒ a = g–1bg for some g ⇒ b = gag–1 = (g–1)–1ag–1 g–1 always exists for every g ∈ G.
- Transitive:aRb and bRc ⇒ a = g1–1bg1 and b = g2–1 cg2 for some g1g2 ∈ G. Now a = g1–1 g2–1 cg2g1 = (g2g1)–1 cg2g1 g1 ∈ G and g2 ∈ G ⇒ g2g1 ∈ G since group is closed so aRb and aRb ⇒ aRc


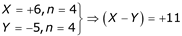 Hence,
Z = 11 which required 5 bits which is (n + 1) bits
Hence,
Z = 11 which required 5 bits which is (n + 1) bits