PREVIOUS YEAR SOLVED PAPERS - GATE 2017 Shift 2
| Character | Probability |
| P | 0.22 |
| Q | 0.34 |
| R | 0.17 |
| S | 0.19 |
| T | 0.08 |
| Total | 1.00 |
If a message of 100 characters over X is encoded using Huffman coding, then the expected length of the encoded message in bits is_____.
Note – Numerical Type question
- Option : A
- Explanation : By using haffman tree :
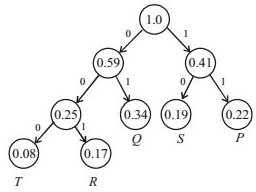 So, number of bit required for each alphabet:
T = 3 bit, R = 3 bit, Q = 2 bit, S = 2 bit, P = 2 bit
Then, average length per character is = (number of bits * frequency of occurance of each alphabets)
= 3 * 0.08 + 3 * 0.17 + 2 * 0.34 + 2 * 0.19 + 2 * 0.22 = 2.25 bits
And, average length for 100 character = 2.25 * 100 = 225 bits.
Hence, 225 bits is correct answer
So, number of bit required for each alphabet:
T = 3 bit, R = 3 bit, Q = 2 bit, S = 2 bit, P = 2 bit
Then, average length per character is = (number of bits * frequency of occurance of each alphabets)
= 3 * 0.08 + 3 * 0.17 + 2 * 0.34 + 2 * 0.19 + 2 * 0.22 = 2.25 bits
And, average length for 100 character = 2.25 * 100 = 225 bits.
Hence, 225 bits is correct answer
52. The next state table of a 2-bit saturating up-counter is given below.
| Q1 | Q0 | Q1+ | Q0+ |
| 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 |
- Option : B
- Explanation : Derivative of gx(z) evaluated at z=1 gives expectation E(X) of X. Therefore, take derivative of gY(z) with respect to z, and plug in z=1 Derivative is N.β.(1 - β + βz)(N-1), plug in z=1, gives Nβ.
55. If the ordinary generating function of a sequence
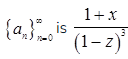 , then a3 - a0 is equal to _____.
, then a3 - a0 is equal to _____.
- Option : A
- Explanation :
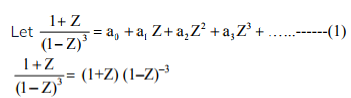 = (1+Z) (1+3Z + 6Z2 + 10Z3 +……….∞)
Using binomial theorem
= 1 + 4Z + 9Z2 + 16Z3 + …… ∞………(2)
From (1) and (2), a0 = 1 and a3 = 16
∴ a3 – a0 = 15
= (1+Z) (1+3Z + 6Z2 + 10Z3 +……….∞)
Using binomial theorem
= 1 + 4Z + 9Z2 + 16Z3 + …… ∞………(2)
From (1) and (2), a0 = 1 and a3 = 16
∴ a3 – a0 = 15


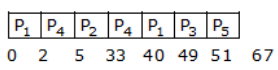 w.t. = 0 + 0 + ( 33 – 5) + (40 – 2) + (49 – 12) + (51 – 9)
= 145
Avg wt = 145/5 = 29
w.t. = 0 + 0 + ( 33 – 5) + (40 – 2) + (49 – 12) + (51 – 9)
= 145
Avg wt = 145/5 = 29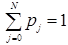 , define the polynomial function
, define the polynomial function 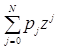 For a certain discrete random variable Y, there exists a scalar β ∈ [0, 1] such that gY(z) = (1 + β + βz)N. The expectation of Y is
For a certain discrete random variable Y, there exists a scalar β ∈ [0, 1] such that gY(z) = (1 + β + βz)N. The expectation of Y is