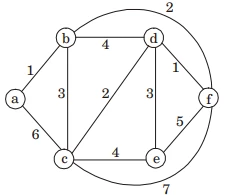
O(m + n) Because, edges are sorted so , no need
to make min heap, so deletion from min heap
time is saved.
Algorithms MCQ - Algorithm Design Techniques
Ordering the weights, the sequence obtained is
1, 1, 2, 2, 3, 3, 4, 4, 5, 6, 7
Now, in order to obtain minimum spanning tree
using Kruskal's algorithm, we have to add edges
with weights in increasing order such that weight
of the spanning tree is minimum.
In option (D), weights of the edges are 1, 1, 2, 3, 2
which contradicts Kruskal's algorithm.
In Kruskal’s Algorithm we choose on edge of G
which has smallest weight among the edges of G.
So (b, e) = 2, (e, f) = 3, (b, c) = 4, (a, c)= 8, (f,g) = 4
(c,d) = 5
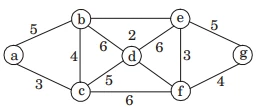
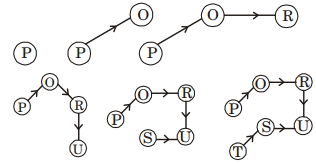
Alternately
Order the edges in non-decreasing order and pick
edge one by one until all the nodes are completed
with no edge making cycle on addition.
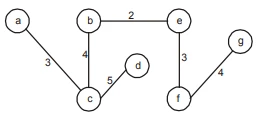
Alternately
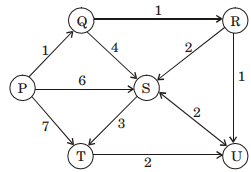
Order the edges in non-decreasing order and pick
edge one by one until all the nodes are completed
with no edge making cycle on addition.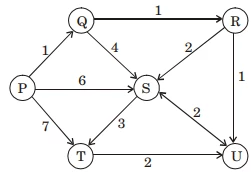
nodes are include in order
⇒ (P, O, R, U, S, T)
