Data Structures and Algorithms - Performance Analysis of Algorithms and Recurrences
- Option : D
- Explanation : The worst case number of comparison is n. to search any element from singly link list.
- Option : A
- Explanation : Note:- In devotion place change first point by 1. (n+k)m = O(nm), where k and m are constants. 1. (n+k)m ≅ O (nm) because k & m are constant then growth rate of both the function is same. 2. 2n+1 ⇒ 2.2n, Here 2 is constant So function is 2n. Statement is true. 3. 22n+1 ⇒ 2.22n ⇒ 2.4n So 4n > 2n then 22n+1 ≠ O(2n).
- Option : B
- Explanation : For large value of y
P = P * (x/i)
S = S + P
When i < y and i + +
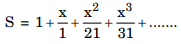 Hence S = ex
Hence S = ex


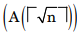 ;
is best described by
;
is best described by