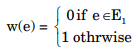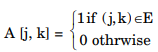Follow Us :

Data Structures and Algorithms - Graph Algorithm

Avatto > > UGC NET COMPUTER SCIENCE > > PRACTICE QUESTIONS > > Data Structures and Algorithms > > Graph Algorithm

16. Consider an undirected unweighted graph G. Let a breadth-first traversal of G be done starting from a node r. Let d(r, u) and d(r, v) be the lengths of the shortest paths from r to u and v respectively in G. If u is visited before v during the breadth first traversal, which of the following statement is correct?

  • Option : C
  • Explanation :
    d(r, v) and d(r, v) will be equal when u and v are at same level, otherwise d (r, v) will be less than d(r, v)
Cancel reply
Cancel reply

17. The Breadth First Search algorithm has been implemented using the queue data structure. One possible order of visiting the nodes of the following graph is

  • Option : C
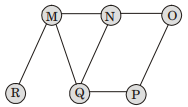
  • Explanation :
    Applying BFS Algorithms
    Starting from Q
    Queue Q
    Making Q’s child’s status 1.
    Queue
    Q| M| N| P
    Making M’s child 1 (which are not 1)
    Status
    QMNOPR
    211 1 
    221 11
    222111
    Q| M| N| P| R
    Making N’s Child 1
    Q| M| N| P| R| O
    (other are already 1)
Cancel reply
Cancel reply

18. Breadth First Search (BFS) is started on a binary tree beginning from the root vertex. There is a vertex t at a distance four from the root. If t is the n-th vertex in this BFS traversal, then the maximum possible value of n is

  • Option : D
  • Explanation :
    Maximum possible value of n for which we have complete tree and our 't' node is the last leaf node at height 4.
    So, the maximum possible value of n
    = 1 + 2 + 4 + 8 + 16
    = 31
Cancel reply
Cancel reply

19. Let G = (V, E) be an undirected graph with a subgraph G1 = (V1, E1). Weights are assigned to edges of G as follows:

A single-source shortest path algorithm is executed on the weighted graph (V, E, w) with an arbitrary vertex v1 of V1 as the source. Which of the following can always be inferred from the path costs computed?

  • Option : B
  • Explanation :
    Suppose G = (v, E) and G1 = (v, E1) such that E1 ≤ E and v1 ≤ v
    Consider an example

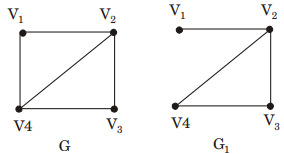    Consider the w(e) = 1 of e ∉ E1 it means the cost of v1 to v4 is only 1 other edges having cost 0. It is noted that G1 is connected (As shown in example).
Cancel reply
Cancel reply

20. Let G = (V, E) be a direction graph with n vertices. A path from vi to v in G is sequence of vertices (vi, 1, ..., such that (vk, vki)E E for all k in i through j — 1. A simple path is a path in which no vertex appears more than once. Let A be an n x n array initialized as follow:

Consider the following algorithm for i = 1 to n for j = 1 to n for k = 1 to n A [j, k] = max (AU, k], (A[j, i] + A[i, k])); Which of the following statements is necessarily true for all j and k after terminal of the above algorithm?

  • Option : D
  • Explanation :
    for i = 1 ton
    for j = 1 ton
    for K = 1 ton
    A[j, K] = max (j, K], A[j, i) + a(i, K)]
    Anxn Matrix and A[j, K] = 1 if (j, K) ∈ E
    so there exist a path from J to K and must contain A[j, K] edges
Cancel reply
Cancel reply
Related Quiz.
Graph Algorithm