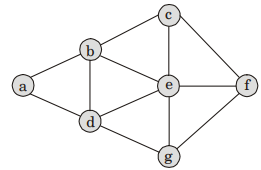
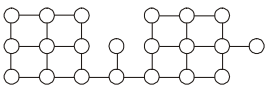
Data Structures and Algorithms - Graph Algorithm
- Option : D
- Explanation : Since d(q) = d(p) + 1 and F(q) < f(P) which means p & q are connected and r is sperate so option (d) is correct answer.
- Option : D
- Explanation :
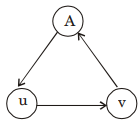Suppose v is starting vertex so start DFS at node v
(i) visit t (v) → DFS(A) → visit (A) → DFS
(v) → visit (u) → back track (A) → Back track (v)
therefore d[v] > d[v], d[v] < f[v] f[v] < f[v]
But visiting order is just opposite of finishing order.
Hence f[v] > f[v]
- Option : D
- Explanation : a b e f d g c, a b e f c g d, a d g e b c f are possible dFs traverse of given graph.
- Option : C
- Explanation : DFS visits each vertex once and as it visits each vertex, we need to find all of its neighbours to figure out where to search next. Finding all its neighbour s in an adjacency matrix r equires O(V) time, so overall the running time will be O(V2).
- Option : A
- Explanation :
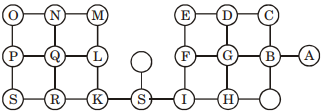Maximum DFS recurside depth is 19
A → B → C → D → E → F → G → H → I → J → K
→ L → M → N → O → P → Q → R → S
