PREVIOUS YEAR SOLVED PAPERS - August 2016 Paper 3
- Option : B
- Explanation : Transformation of an object point Q(x, y), θ° about a fixed center of rotation P(h, k)
step 1: Translate so that the center of rotation P is at the origin
step 2: Perform a rotation of θ° about the origin, and
step 3: Translate P back to (h, k)
using V = hi + kj as translation vector
Rθ,P = T-v Rθ Tv
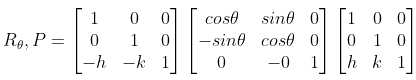θ = 60°, h = 1, k = 2, Q(x, y) = (2, 5)
Q' = Q.R60,P
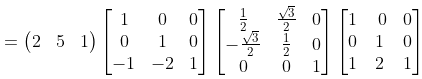
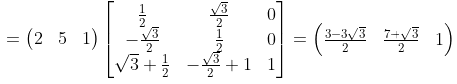
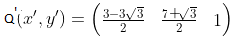so,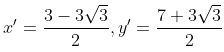 
x' = (3-5.196)/2 = -2.196/2 = -1.098 ≅ -1
y' = (7+1.732)/2 = 8.1732/2 = 4.0866 ≅ 4
So, option (B) i.e (-1, 4) is the answer
- Option : C
- Explanation :
- In perspective projection (from 3D to 2D), objects behind the centre of projection are projected upside down and backward onto the view-plane. This is known as view confusion.
- Vanishing point: Where all parallel points appear to meet is called vanishing point.
- Perspective foreshortening: As we move from centre of projection size of object varies inversely with distance, this is known as perspective foreshortening.
- Topological Distortion: A line segment joining a point lying in front of the viewer to a point in back of the viewer is projected to a broken line of infinite extent.This is known as topological distortion.
So, option (C) is correct.
- Option : B
- Explanation : first we will calculate ∆x and ∆y: i.e. ∆x = x2– x1 = 11 - ( - 1) = 11 + 1 = 12. ∆y = y2– y1 = 1 - 7 = - 6 Now P1 = -∆x = - 12 P2 = ∆x = 12 P3 = -∆y = 6 P4 = ∆y = - 6 Q1 = x1 - xmin = - 1 - 1 = -2 Q2 = xmax - x1 = 9 - ( - 1) = 9 + 1 = 10. Q3 = y1 - ymin = 7 - 2 = 5. Q4 = ymax - y1 = 8 -7 = 1. P1, P4 < 0 and P2, P3 > 0. Intially: t1 = 0, t2 = 1 t1 = max(0, Q1 / P1, Q4 / P4) = max(0, 2 / 12, 1 / -6) = 1 / 6. t2 = min(1, Q1 / P1, Q4 / P4) = min(1, 10 / 12, 5 /6). = 5 / 6. i.e. u ranges between (1 / 6, 5 / 6). So, option (B) is correct.
19. Match the following with reference to Functional programming history:
| a. Lambda calculus | i. Church, 1932 |
| b. Lambda calculus as programming language | ii. Wordsworth, 1970 |
| c. Lazy evaluation | iii. Haskel, 1990 |
| d. Type classes | iv. Mecarthy, 1960 |
Codes:
| a | b | c | d | |
| (1) | iv | i | iii | ii |
| (2) | i | iv | ii | iii |
| (3) | iii | ii | iv | i |
| (4) | ii | i | iv | iii |
- Option : B
- Explanation :
- Lambda calculus was introduced by Alonzo Church in 1932.
- Lambda calculus as programming language applied by Mecarthy in 1960
- Lazy evaluation was introduced by Wordsworth in 1970
- Type classes was introduced by Haskel in 1990
So, option (B) is correct.
