PREVIOUS YEAR SOLVED PAPERS - GATE 2020
- Option : D
- Explanation : Main memory access time, Tm = 100 ns
TLB lookup, TTLB = 20ns
Page transfer time, TPT = 5000 ns
TLB hit ratio, x = 0.95 (95%) page fault rate, p = 0.10 (10%)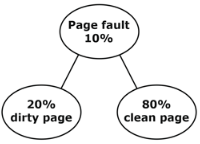 We know,
EMAT for multilevel paging,
EMAT = x (Tc + Tm) + (1 – x) (Tc + (n + 1) Tm)
EMAT, when there is a page fault, S → is service time
EMAT = (1 – P) Tm + Ps
Here, we are using TLB, and page fault occurs whenever there is a miss in TLB, So the required EMAT is ,
EMAT = x(Ttlb + Tm) + (1 – x) [(1 – P) (Ttlb + Tm + Tm) + p(% dirty (Ttlb + Tm + 2TPT) + % clean (Ttlb + Tm + TPT)
∴ EMAT = 0.95 (20 + 100) + 0.05 (0.9 (20 + 100 + 100) + 0.1 (0.2 (20 + 100 + 2(5000)) + 0.8 (20 + 100 + 5000))
= 154.5 ns
We know,
EMAT for multilevel paging,
EMAT = x (Tc + Tm) + (1 – x) (Tc + (n + 1) Tm)
EMAT, when there is a page fault, S → is service time
EMAT = (1 – P) Tm + Ps
Here, we are using TLB, and page fault occurs whenever there is a miss in TLB, So the required EMAT is ,
EMAT = x(Ttlb + Tm) + (1 – x) [(1 – P) (Ttlb + Tm + Tm) + p(% dirty (Ttlb + Tm + 2TPT) + % clean (Ttlb + Tm + TPT)
∴ EMAT = 0.95 (20 + 100) + 0.05 (0.9 (20 + 100 + 100) + 0.1 (0.2 (20 + 100 + 2(5000)) + 0.8 (20 + 100 + 5000))
= 154.5 ns
- Option : A
- Explanation : If we consider a small graph with 5 vertices, then the minimum spanning tree will have a weight 4. So, for n-vertices, MST weight would be (n – 1) As n = 100 (no. of vertices), So, minimum spanning tree weight = (100 – 1) = 99
- Option : A
- Explanation : Min-heap contains 1023 elements.
Min-heap means, parent should be minimum or equal to it’s children so, max children could be either left or right one.
Following this logic, maximum can be definitely at leaf nodes.
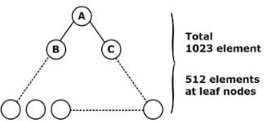 No. of elements in leaf = n/2 = 1023/2 = 512
To find maximum among 512 elements, no. of comparisons needed is 511.
No. of elements in leaf = n/2 = 1023/2 = 512
To find maximum among 512 elements, no. of comparisons needed is 511.
- Option : B
- Explanation : Non-pipeline
Clock frequency = 2.5 GHz.
Cycle time = 1/2.5 GHz = 0.4ns
Given, CPI = 5
So, ETnon-pipe = CPI × Cycle time
= 5 × 0.4 ns = 2 ns
Pipeline:
Clock frequency = 24 GHz
Cycle time = 1/2 GHz = 0.5ns
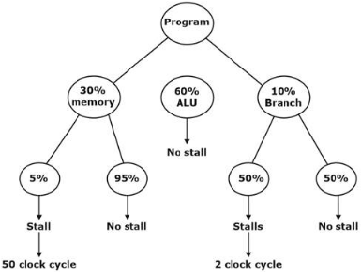 ∴ Number of stalls/instruction = 0.3 × 0.05 × 50 + 0.1 * 0.5 × 2
= 0.85
Avg. instruction ETpipe = (1 + No. of stall instruction) * cycle time
= (1 + 0.85) × 0.5 ns = 0.925 ns
∴ Number of stalls/instruction = 0.3 × 0.05 × 50 + 0.1 * 0.5 × 2
= 0.85
Avg. instruction ETpipe = (1 + No. of stall instruction) * cycle time
= (1 + 0.85) × 0.5 ns = 0.925 ns
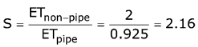


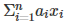 is an number is _______ .
is an number is _______ .
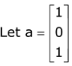 x = 0 or 1
x = 0 or 1
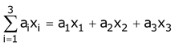 = x1 = x3 (∵ a1 = 1, a2= 0, a3 = 1)
= 0 or 1 or 1 or 2.
= x1 = x3 (∵ a1 = 1, a2= 0, a3 = 1)
= 0 or 1 or 1 or 2.
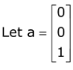
 Total number of cases = 2 × 3 + 4 × 3 = 18
Now odd number of cases = 9
P = 9/18 = 0.5
Total number of cases = 2 × 3 + 4 × 3 = 18
Now odd number of cases = 9
P = 9/18 = 0.5