PREVIOUS YEAR SOLVED PAPERS - GATE 2017 Shift 2
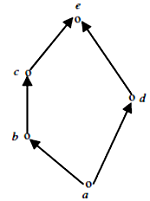
- Option : A
- Explanation : A Hasse Diagram is called a Lattice, if for every pair of elements there exists a LUB and GLB. In the above Hasse Diagram, LUB and GUB exist for every two elements taken from {a,b,c,d,e}. So, it is already a Lattice. Hence, Minimum number of ordered pairs that need to be added =0
- Option : A
- Explanation : Bottom up parsers in decreasing order of their power: CLR≫ LALR≫ SLR≫ LR (0) The given statements: I. Canonical LR is more powerful than SLR is CORRECT. II. SLR is more powerful than LALR is INCORRECT III. SLR is more powerful than Canonical LR is INCORRECT.
| P. | Static char var; | i. | Sequence of memory locations to store addresses |
| Q. | m = malloc (10); m = NULL: | ii. | A variable located in data section of memory |
| R. | R. char * ptr [10] | iii. | Request to allocate a CPU register to store data |
| S. | Register int var1; | iv. | A lost memory which cannot be freed |
- Option : A
- Explanation : P. static char var: var is defined as character variable whose associated storage class is static because of this it is given memory from data segment Q. m malloc(10); m = NULL; 10 contiguous bytes of memory is allocated is address of first byte is stored in 'm' and later it is updated with NULL. Now we lost the address of first bytes of that chunk of memory completely. So we can't free that space as we need the address of first byte to free it up R. char * ptr [10]: ptr is an array of 10 pointers pointing to character variables. S. register int varl: Suggesting the complier to store the var1 “value” in CPU register.
- Option : B
- Explanation : Given L1 and L2 are context free languages and R is a regular language. I. L1 ∪ L2 is context free is CORRECT, context free language are closed under union operation. II. L1 is context free is INCORRECT, context free languages are not closed under complement operation. III. L1 - R is Context free is CORRECT. L1 - R = L1 ∩ R, Context free intersection Regular is always Context free. IV. L1 ∩ L2 is context free is INCORRECT; context free languages are not closed under complement operation.
