PREVIOUS YEAR SOLVED PAPERS - GATE 2017 Shift 2
46. Consider the recurrence function
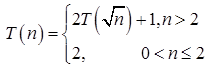Then T(n) in terms of θ notation is
- Option : B
- Explanation : T(n) = 2T(√n) + 1
Put n = 2K
T(2K) = 2T(2K/2) + 1
T(2K) = δ(K)
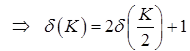By master's theorem
δ(K) = θ(K)
T(2K) = θ(K)
T(n) = θ(log n) ∵ 2K = n
- Option : A
- Explanation : Using Linearity of Expectation, we can write, E[(X+2)2] = E[X2] + E[4X] + E[4] The Poisson distribution, mean and variance are same. Here Mean is given as 5. So variance should also be 5. Also, Variance = E[X2] – (E[X])2 5 = E[X2] – 25. E[X2] = 30 Thus E[(X+2)2] = 30 + 4*5 + 4 = 54.
- Option : C
- Explanation : for i = 1 j will run from 1 to n by incrementing by '1' in each step 'j 'will run for n times For i=2 j will run from 1 to n by incrementing by ‘2’ in each step j will run for n/2 times next time j will run for n/3 times and so on time complexity = n + n/2 + n/3 + n/4 + ..... = n(1+1/2+1/3+.....) =nlogn
- Option : B
- Explanation : Given: Preorder ! 12, 8, 6, 2, 7, 9, 10, 16, 15, 19, 17, 20
In order! 2, 6, 7, 8, 9, 10, 12, 15, 16, 17, 19, 20
Note: BST In order will give ascending order
Corresponding BST is
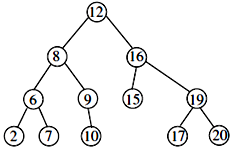∴ Post order is 2, 7, 6, 10, 9, 8, 15, 17, 20, 19, 16, 12
- Option : C
- Explanation : Given, program is: (while (r y){ } If we want to final value as Then initial value of r should be equal to x (Since y is subtracted from r each time in given code). q incremented by 1 (q is quotient here). To avoid undefined behavior, value of y should be greater than zero. Therefore, (q == 0)&&(r == x)&&(y > 0))
