Algorithms - Algorithm Design Techniques
- Option : D
- Explanation : Minimum number of edges for a connected
graph = n
and for a connected tree = n – 1
 Here given that 2 n – 2 edges and the edges of
graph is partitioned into two edge disjoint trees.
So there are two vertex disjoint paths between
every pair of vertices.
Here given that 2 n – 2 edges and the edges of
graph is partitioned into two edge disjoint trees.
So there are two vertex disjoint paths between
every pair of vertices.
- Option : B
- Explanation : Using concepts of Dynamic Programming to find the maximum possible weight of a subsequence of X, we will have two alternatives. 1. Do not include a0 in the subsequence: then the maximum possible weight will be equal to maximum possible weight of a subsequence of {a1, a2....an} which is represented by Y. 2. Include a0: then maximum possible weight will be equal to a0 + (each number picked om Y will get divided by 2) a0 + Y/2. Here you can note that Y will itself pick optimal subsequence to maximum the weight. Final answer will be Max (Case1, Case2) i.e. Max (Y, a0 + Y/2). Hence B.
Common Data for Questions 28 and 29
Consider a complete undirected graph with vertex set {0, 1, 2, 3, 4}. Entry Wij in the matrix W below is the weight of the edge {i, j}.
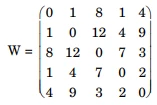
Linked Data Question 30 and 31
An undirected graph G(V, E) contains n(n > 2) nodes named v1 , v2 , …, vn . Two nodes vi , vj are connected if and only if 0 < | i – j | ≤ 2. Each edge (vi , vj ) is assigned a weight i + j. A sample graph with n = 4 is shown below.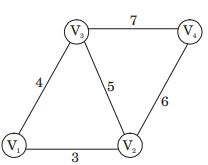
30. What will be the cost of the Minimum Spanning Tree (MST) of such a graph with n nodes?
- Option : B
- Explanation : If we construct graph for n = 6 vertices
(V1
, V2
, V3
, V4
, V5
, V6
)
then minimum spanning tree for this graph is
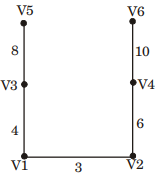 total weight = 31
so if we put n = 6 in option “b” then we get 31
i.e. x2 – n + 1
(6)2 – 6 + 1 ⇒ 36 – 6 + 1 ⇒ 31.
total weight = 31
so if we put n = 6 in option “b” then we get 31
i.e. x2 – n + 1
(6)2 – 6 + 1 ⇒ 36 – 6 + 1 ⇒ 31.


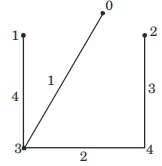 total weight = 4 + 1 + 2 + 3 = 10
total weight = 4 + 1 + 2 + 3 = 10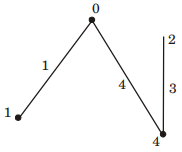 Path from vertex 1 to 2 is
(1 – 0) + (0 – 4) + (4 – 2)
1 + 4 + 3 = 8
Path from vertex 1 to 2 is
(1 – 0) + (0 – 4) + (4 – 2)
1 + 4 + 3 = 8