Algorithms - Algorithm Design Techniques
- Option : C
- Explanation : In adjacency matrix if diagonal elements are 0’s and non-diagonal are 1’s then it is complete graph and in complete graph of n vertices total nn–2 Spanning trees are possible and cost of each tree. is (n – 1) because for n vertex graph, (n – 1) edges required in a tree.
You must be logged in to post a comment.
- Option : A
- Explanation : Option A is correct, there exists a cut set in G having all edges of maximum weight
You must be logged in to post a comment.
You must be logged in to post a comment.
- Option : B
- Explanation : Minimum spanning tree of such a graph is
Weight of the minimum spanning tree
= 2|2 – 1| + 2|3 – 2| + 2|4 – 3| + 2|5 – 4| …. + 2| n – (n-1) |
= 2n – 2
You must be logged in to post a comment.
You must be logged in to post a comment.
- Option : D
- Explanation : e is needed not to be present in every spanning tree since there may be edges (in cycle formed by adding e), which has same weight as e has.
You must be logged in to post a comment.
You must be logged in to post a comment.
Common Data for Q. 25 & Q. 26
Suppose the letters a, b, c, d, e have probabilities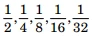
respectively
- Option : C
- Explanation :
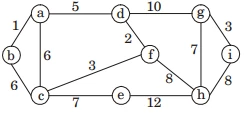
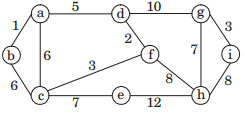In prims algorithm we can select arbitary vertex
and them, find all the edges that connect the tree
to new vertex and find the minimum and add it
to the tree. So option “C” is correct
(d, f), C), (d, a), (a, b), (c, e), (F, h), (g, h) (g, i).
You must be logged in to post a comment.
You must be logged in to post a comment.
You must be logged in to post a comment.