Algorithms - Algorithm Design Techniques
- Option : A
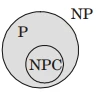
- Explanation : 1. We can use “Depth First Search” Algorithm, to check it there is a cycle is an undirected graph. I t we encounter any “back edge” in “Depth first search” then given undirected graph has a cycle. Also, If there is a cycle in the Undirected graph, we must encounter a “back edge” in DFS. And, DFS can be done in O(| E| + | V| ) time for graph G = (V, E). So, it can is in F. 2. P ≤ NP, So, it is also in NP. 3. NP - complete problem A ∈ NP. By, Definition Every problem in NP can be solved in polynomial time using non-deterministic turing machine. So, Answer is (A) i.e. 1, 2, and 3 are true.
- Option : D
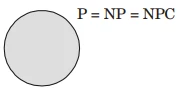
- Explanation : The most important open question in complexity t heor y is whether the P = NP, which asks whether polynomial time algorithms actually exist for NP-complete and all NP problems (since a problem “C” is in NP-complete, iff C is in NP and every problem in NP is reducible to C in polynomial time). In the given question it is given that some polynomial time algorithm exists which computes the largest clique problem in the given graph which is known NP-complete problem. Hence P = NP = NP-Complete.
- Option : B
- Explanation : 2CNF SAT can be solvable in polynomial time by reduction to directed graph reach ability.
