Algorithms - Algorithm Design Techniques
60. Let πA be a problem that belongs to the class NP. Then which one of the following is TRUE?
- Option : D
- Explanation : If πA is NP-hard, then it is NP-complete Alternately πA be a problem (given) in class NP. we say that πA is NP complete if the following statements are true about L. (1) πA is in NP (2) For every πA'in NP there is polynomial time reduction of πA' to πA.



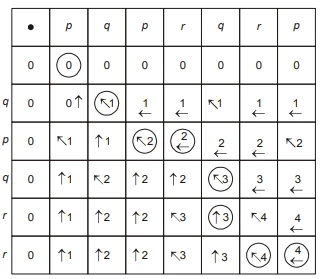 Longest common subsequence : qpqr
x + 10y = 4 + 10 × 3 = 34
Longest common subsequence : qpqr
x + 10y = 4 + 10 × 3 = 34