If the post order traversal gives a b - c d * + then the label of the nodes 1, 2, 3 ... will be
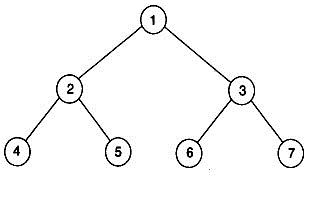
| A. | +, -, *, a, b, c, d |
| B. | a, -, b, +, c, *, d |
| C. | a, b, c, d, -, *, + |
| D. | -, a, b, +, *, c, d |
|
Option: A Explanation : Post-order traversal yields 4, 5, 2, 6, 7, 3, 1. Comparing with a, b, -, c, d, *, +, we get the labels of nodes 1, 2, 3, 4, 5, 6, 7 ans +, -, *, a, b, c, d respectively. Click on Discuss to view users comments. |
Consider the following tree
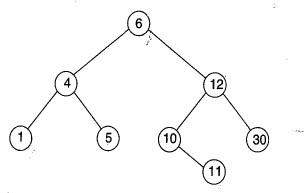
If this tree is used for sorting, then a new number 8 should be placed as the
| A. | left child of the node labeled 30 |
| B. | right child of the node labeled 5 |
| C. | right child of the node labeled 30 |
| D. | left child of the node labeled 10 |
|
Option: D Explanation : If it is to be used for sorting label of left child should be less than the label of the current node. Coming down the tree we get left child of node labeled 10 as the correct slot for 8. Click on Discuss to view users comments. |
The number of possible ordered trees with 3 nodes A, B, C is
| A. | 16 |
| B. | 12 |
| C. | 6 |
| D. | 10 |
|
Option: B Explanation : It is 12. The tree may be of depth 2 or 1. if the depth is 2, we have 6 possible trees. This is because one of the three nodes A, B, C may be the root and the next level may be one of the remaining two nodes. If the depth is 1, the root may be one of the 3 nodes A, B, C. Corresponding to a root, say A, two trees as possible as this. Click on Discuss to view users comments. |
A binary tree in which every non-leaf node has non-empty left and right subtrees is called a strictly binary tree. Such a tree with 10 leaves
| A. | cannot have more than 19 nodes |
| B. | has exactly 19 nodes |
| C. | has exactly 17 nodes |
| D. | cannot have more than 17 nodes |
|
Option: B Explanation :
Click on Discuss to view users comments. |