Theory of Computation and Compilers - Syntax Analysis
- Option : A
- Explanation : The grammar is S → AC/CB C → aCb/ε A → aA/a B → Bb/b and number of derivation step is max(l, m) + 2
Consider the CFG with {S, A, B} as the non-terminal alphabet, {a, b} as the terminal alphabet, S as the start symbol and the following set of production rules
| S → bA | S → aB |
| A → a | B → b |
| A → aS | B → bS |
| A → bAA | B → aBB |
Consider the CFG with {S, A, B} as the non-terminal alphabet, {a, b} as the terminal alphabet, S as the start symbol and the following set of production rules
| S → bA | S → aB |
| A → a | B → b |
| A → aS | B → bS |
| A → bAA | B → aBB |
For the grammar below, a partial LL(1) parsing table is also presented along with the grammar. Entries that need to be filled are indicated as E1, E2, and E3. ε is the empty string, $ indicates end of input, and | separates alternate right hand sides of productions. S → a A b B|b A a B|ε A → S B → S a b $ S E1 E2 S → ε A A → S A → S error B B → S B → S E3
9. The FIRST and FOLLOW sets for the nonterminals A and B are
- A
FIRST (A) = {a, b, ε} = FIRST (B), FOLLOW (A) = {a, b} FOLLOW (B) = {a, b, $}


- B
FIRST (A) = {a, b, $} FIRST (B) = {a, b, ε} FOLLOW (A) = {a, b} FOLLOW(B) = {$}


- C
FIRST (A) = {a, b, ε} = FIRST (B), FOLLOW (A) = {a, b} FOLLOW (B) = $


- D
FIRST (A) = {a, b} = FIRST (B) FOLLOW (A) = {a, b} FOLLOW (B) = {a, b}


- Option : A
- Explanation : FIRST(S) = {a, b, ε} FIRST(A) = FIRST(S) = {a, b, ε} FIRST(B) = FIRST(S) = {a, b, ε} FOLLOW (A) = {b, a} FOLLOW (S) = {$} U FOLLOW (A) = {b, a, $} FOLLOW (B) = FOLLOW (S) = {b, a, $}
For the grammar below, a partial LL(1) parsing table is also presented along with the grammar. Entries that need to be filled are indicated as E1, E2, and E3. ε is the empty string, $ indicates end of input, and | separates alternate right hand sides of productions. S → a A b B|b A a B|ε A → S B → S a b $ S E1 E2 S → ε A A → S A → S error B B → S B → S E3
10. The appropriate entries for E1, E2 and E3 are
- Option : C
- Explanation : E1 : M[S, a] : S → aAbB, S → ε (because first of S contain a and ε) E2 : M[S, b] : S → bAaB, S → ε (because first of S contain b and ε) E3 : M[b, $] : B → S (because first of B contain ε)
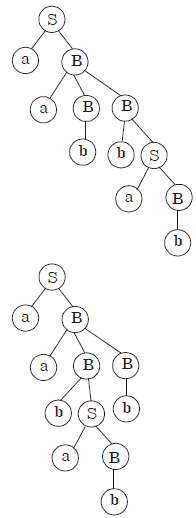 two parse tree.
two parse tree.