Follow Us :

PREVIOUS YEAR SOLVED PAPERS - November 2017 Paper 3

Avatto > > UGC NET COMPUTER SCIENCE > > PREVIOUS YEAR SOLVED PAPERS > > November 2017 Paper 3

31. Consider a full binary tree with n internal nodes, internal path length i, and external path length e. The internal path length of a full binary tree is the sum, taken over all nodes of the tree, of the depth of each node. Similarly, the external path length is the sum, taken over all leaves of the tree, of the depth of each leaf. Which of the following is correct for the full binary tree?

Cancel reply

Your email address will not be published. Required fields are marked *


Cancel reply

Your email address will not be published. Required fields are marked *


32. You are given a sequence of n elements to sort. The input sequence consists of n/k subsequences,each containing k elements. The elements in a given subsequence are all smaller than the elements in the succeeding subsequence and larger than the elements in the preceding subsequence. Thus, all that is needed to sort the whole sequence of length n is to sort the k elements in each of the n/k subsequences. The lower bound on the number of comparisons needed to solve this variant of the sorting problem is

Cancel reply

Your email address will not be published. Required fields are marked *


Cancel reply

Your email address will not be published. Required fields are marked *


33. Consider the recurrence relation:


 Where b and c are constants. The order of the algorithm corrosponding to above recurrence relation is:

  • Option : D
  • Explanation :
    We can use Master theorem to solve this recurrance relation:T(n) = aT(n/2) + Θ(nklogpn)
    In given question:
    T(n) = 8T(n/2) + Cn
    here a = 8 and b = 2 and k = 1.
    clearly a > bk
    So T(n) = Θ(nlogba )
    T(n) = Θ(nlog2 8)
    ie T(n) = Θ(n3)
    So, option (D) is correct.
Cancel reply

Your email address will not be published. Required fields are marked *


Cancel reply

Your email address will not be published. Required fields are marked *


34. Consider the following two sequences :
X = < B, C, D, C, A, B, C >, and
Y = < C, A, D, B, C, B >
The length of longest common subsequence of X and Y is :

Cancel reply

Your email address will not be published. Required fields are marked *


Cancel reply

Your email address will not be published. Required fields are marked *


35. A text is made up of the characters a, b, c, d, e each occurring with the probability 0.11, 0.40, 0.16, 0.09 and 0.24 respectively. The optimal Huffman coding technique will have the average length of:

  • Option : B
  • Explanation :
    a = 0.11 b = 0.40 c = 0.16 d = 0.09 e = 0.24 we will draw a huffman tree:
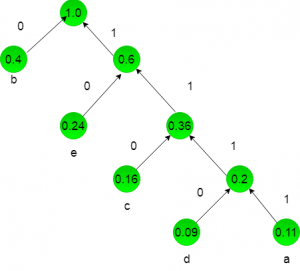    Nov2017 cs
    now huffman coding for character:
    a = 1111, b = 0, c = 110, d = 1111, e = 10
    lenghth for each character = no of bits * frequency of occurence:
    a = 4 * 0.11 = 0.44
    b = 1 * 0.4 = 0.4
    c = 3 * 0.16 = 0.48
    d = 4 * 0.09 = 0.36
    e = 2 * 0.24 = 0.48
    Now add these lenght for average length: 0.44 + 0.4 + 0.48 + 0.36 + 0.48 = 2.16
Cancel reply

Your email address will not be published. Required fields are marked *


Cancel reply

Your email address will not be published. Required fields are marked *


Related Quiz.
November 2017 Paper 3