PREVIOUS YEAR SOLVED PAPERS - July 2016 Paper 3
- Option : B
- Explanation : The region of feasible solution of a linear programming problem has a convexity property in geometry, provided the feasible solution of the problem exists. Convexity is a measure of the curvature in the relationship between prices and yields. Other term doesn't related to linear programming problem. So, option (B) is correct.
- Option : D
- Explanation :
- Revised simplex method requires lesser computations than the simplex method.Correct
- Revised simplex method automatically generates the inverse of the current basis matrix.Correct
- Less number of entries are needed in each table of revised simplex method than usual simplex method.Correct All statement are correct.
So, option (D) is correct.
63. The following transportation problem:
| A | B | C | Supply | |
| I. | 50 | 30 | 220 | 1 |
| II. | 90 | 40 | 170 | 3 |
| III. | 250 | 200 | 50 | 4 |
| Demand | 4 | 4 | 2 |
has solution
| A | B | C | |
| I. | 1 | ||
| II. | 3 | 0 | |
| III. | 2 | 2 |
and
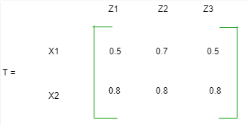
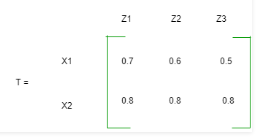
- Option : D
- Explanation : Since x is related to y and y is related to z, to relate universe x and universe z we have to compute max-min composition: x1z1= max(min(0.7, 0.9), min(0.5, 0.1)) = max(0.7 0.1) = 0.7 x1z2= max(min(0.7, 0.6), min(0.5, 0.7)) = max(0.6, 0.5) = 0.6 x1z3= max(min(0.7, 0.2), min(0.5, 0.5)) = max(0.2, 0.5) = 0.5 x2z1= max(min(0.8, 0.9), min(0.4, 0.1)) = max(0.8, 0.1) = 0.8 x2z2= max(min(0.8, 0.6), min(0.4, 0.7)) = max(0.6, 0.4) = 0.6 x3z3= max(min(0.8, 0.2), min(0.4, 0.5)) = max(0.2, 0.4) = 0.4 So, option (C) is correct.
- Option : D
- Explanation : According to question: A={(0.3, 1), (0.6, 2), (1, 3), (0.7, 4), (0.2, 5)} B={(0.5,11), (1, 12), (0.5, 13)} first add the numbers(x + y = z) and write the min membership value since function is min((μA(x),μB(x)) u will get following 15 terms: {(0.3, 12), (0.3, 13), (0.3, 14), (0.5, 13), (0.6, 14), (0.5, 15), (0.5, 14), (1, 15), (0.5, 16), (0.5, 15), (0.7, 16), (0.5, 17), (0.2, 16), (0.2, 17), (0.2, 18) f(A + B) is equal to {(0.3, 12), (0.5, 13), (0.6, 14), (1, 15), (0.7, 16), (0.5, 17), (0.2, 18)} So, option (D) is correct.
