uptetd16p2 q123

0. The diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If ∠DAC = 32⁰, ∠AOB = 70⁰, Then ∠DBC is equal to

Answer
Comment
Array

Option : C
Explanation : (C)

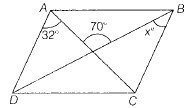
∠DAC = 32⁰ and ∠AOB = 70⁰ (given)
∠BOC + ∠AOB = 180⁰ [∵ Liner pair]
⇒ ∠BOC + 70⁰ = 180⁰
⇒ ∠BOC = 180⁰ - 70⁰ = 110⁰
∠ACB = ∠DAC [∵ Alternate angles between the parallel lines]
⇒ ∠ACB = 32⁰ [∵ ∠DAC = 32⁰ (given)]
or ∠OCB = 32⁰
Now, in △OCB, ∠OCB + ∠BOC + ∠OBC = 180⁰ [∵ Angle sum property of a triangle]
⇒ 32⁰ + 110⁰ + ∠OBC = 180⁰
⇒ ∠OBC = 180⁰ - (110⁰ + 32⁰)
⇒ ∠OBC = 38⁰ = x

Forgot your password?

I agree with the Terms.