uptetd16p1 q104
- Option : C
- Explanation : (C)
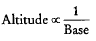
∴ Shortest base have longest altitude.
Side of a triangle are 35 cm, 54 cm, and 61 cm (given)
∴ Altitude corresponding to base 35 cm is the longest.
According to the figure,
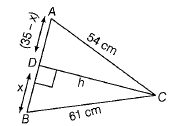
In △ADC,
(54)2 = h2 + (35 - x)2 [by Pythagoras theorem]
⇒ h2 = (54)2 - (35 - x)2 .......(i)
In △BDC,
(61)2 = h2 + x2
⇒ h2 = (61)2 - x2
⇒ (54)2 - (35 - x)2 = (61)2 - x2 [by Eq.(i)]
⇒ 2916 - (1225 + x2 - 70x) = 3721 - x2
⇒ 2916 - 1225 - x2 + 70x = 3721 - x2
⇒ 70x = 3721 - 2916 + 1225
⇒ x = 29
Now, we know that
(61)2 - x2 = h2 ⇒ (61)2 - (29)2 = h2
⇒ h2 = 2880 ⇒ h = 24√5 cm
∴ Lenght of the longes altitude is 24√5 cm.


