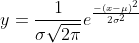UGC NET COMMERCE December 2018 Q66
0. Which one of the following is not the correct property of normal distribution?
- Option : C
- Explanation : Properties of a Normal Distribution
A normal Distribution is a continuous probability distribution for a random variable x. The graph of a normal distribution is called the normal curve, which has all of the following properties:
1. The mean, median and mode are equal.
2. The normal curve is bell-shaped and is symmetric about the mean.
3. The total area under the curve is equal to one.
4. The normal curve approaches, but never touches the x-axis.
5. Between μ – σ and μ + σ the graph is concave down and elsewhere the graph is concave up. The points at which the graph changes concavity are called inflection points.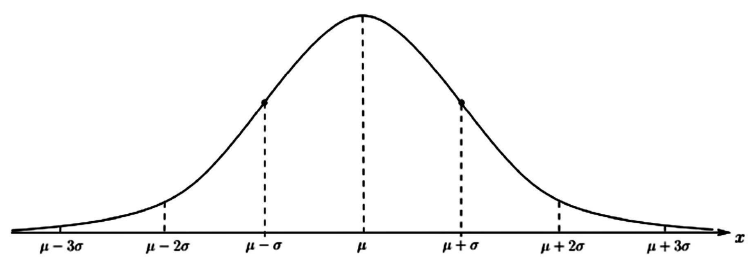
Remarks
∎ A normal distribution can have any mean and any positive standard deviation
∎ The two parameters, μ and s completely determine the shape of the normal curve.
∎ The equation of the normal curve is