PA of Algorithms Q33
- Option : C
- Explanation : Recurrance relation for procedure A (n) is T(n) = T √n + 1 if n > 2 T(n) = 1 if n ≤ 2 T(n) = 1 Now, T (n) = T √n + 1 Put n = 2k, T (2k)= T (2k/2) + 1 Use S(K) for T (2k) then S(K) = S(k/2) + 1 Apply masters method. Klog21 ≅ 1 So θ (log k) Now we know that n = 2k so, k= log2n So, O(log logn).
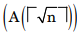 ;
is best described by
;
is best described by

