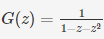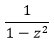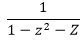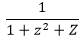PA of Algorithms Q27
0. What is the generating function G(z) for the sequence of Fibonacci numbers?
- Option : C
- Explanation : Assuming Fibonacci Sequence as :- 1, 1, 2, 3, 5, 8, 13, ......
So, sequence an = 1,1,2,3,5,8,13,… where, n=0,1,2,3,…
Now, The Generating Function for the sequence an of real numbers is defined as:
So, For the given Fibonacci Series :-
⇒ G(z) = 1+z+2z2+3z3+5z4+8z5+13z6+...+fnzn+... →(1)
Now , Shift one position right and multiply by 'z' :-
⇒ zG(z) = z+z2+2z3+3z4+5z5+8z6+... →(2)
Now, Shift one more position right and multiply by 'z' :-
⇒ z2G(z)=z2+z3+2z4+3z5+5z6+8z7+... →(3)
Now, Add Equation(2) and Equation(3) :-
⇒ zG(z)+z2G(z)=z+2z2+3z3+5z4+8z5+13z6+...
⇒ zG(z)+z2G(z)=G(z)−1 (From(1))
⇒ G(z)−zG(z)−z2G(z)=1
⇒
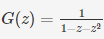So,Generating Function for the given Fibonacci Series is:−
