Graph Algorithm 12

0. A depth-first search is performed on a directed acyclic graph. Let d[u] denote the time at which vertex u is visited for the first time and f[u] the time at which the dfs call to the vertex u terminates. Which of the following statements is always true for all edges (u, v) in the graph?

Answer
Comment
Array

Option : D
Explanation :

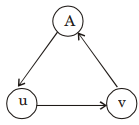Suppose v is starting vertex so start DFS at node v
(i) visit t (v) → DFS(A) → visit (A) → DFS (v) → visit (u) → back track (A) → Back track (v)
therefore d[v] > d[v], d[v] < f[v] f[v] < f[v]
But visiting order is just opposite of finishing order.
Hence f[v] > f[v]

Forgot your password?

I agree with the Terms.