Follow Us :

Gate2019 cs Q58

0. Let Σ be the set of all bijections from {1,…,5} to {1,…,5}, where 𝑖𝑑 denotes the identity function, i.e. id(j) =j,∀j. Let ∘ denote composition on functions. For a string 𝑥 = 𝑥1 𝑥2 ⋯ 𝑥n ∈ Σsup>1, 𝑛 ≥ 0, let (𝑥) = 𝑥1 ∘ 𝑥2 ∘ ⋯ ∘ 𝑥n.
Consider the language 𝐿 = {𝑥 ∈ Σ∗| (𝑥) = 𝑖𝑑}. The minimum number of states in any DFA accepting L is _________.

  • Option : A
  • Explanation :
    The DFA for accepting L will have 5! = 120 states, since we need one state for every possible permutation function on 5 elements. The starting state will be “id” state, named as Gate2017 cs and from there
    n! arrows will go the n! states each named with a distinct permutation of the set {1, 2, 3, 4, 5}. Since composition of permutation function is closed every arrow has to go to some permutation and hence some state.
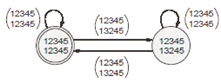
    Since the language only has those strings where π(x) = id only the starting state (“id” state) will be the final state. Sample machine with only 2 states is shown below
    Gate2017 cs
Cancel reply

Your email address will not be published. Required fields are marked *


Cancel reply

Your email address will not be published. Required fields are marked *