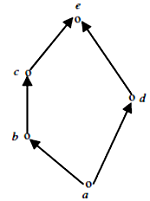
Gate2017 ss Q11

0. Consider the set under the partial ordering R = {(a,a),(a,b),(a,c),(a,d),(a,e),(b,b),(b,c),(b,e),(c,c),(c,e),(d,d),(d,e),(e,e)}. The Hasse diagram of the partial order (X, R) is shown below.

The minimum number of ordered pairs that need to be added to R to make (X, R) a lattice is _____.

Note – Numerical Type question

Answer
Comment
Array

Option : A
Explanation :
A Hasse Diagram is called a Lattice, if for every pair of elements there exists a LUB and GLB.
In the above Hasse Diagram, LUB and GUB exist for every two elements taken from {a,b,c,d,e}. So, it is already a Lattice.
Hence, Minimum number of ordered pairs that need to be added =0

Forgot your password?

I agree with the Terms.