Algorithms - Algorithm Design Techniques
31. The length of the path from v5 to v6 in the MST of previous question with n = 10 is
- Option : C
- Explanation : Length of path V5
to V6
in mst of n = 10 vertices is
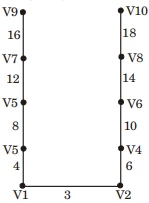 Path from V5
to V6 contain 8+4+3+6+10 = 31
Path from V5
to V6 contain 8+4+3+6+10 = 31
- Option : A
- Explanation : Minimum sparring tree of G does not change,
because every edge weight is positive and distinct,
so to increase the value of each edge by same
constant value it does not change tree.
Q is false because path may be change. Here path
from B to C can. be via A but after increase by 1
path must be from B to C direct.
Example
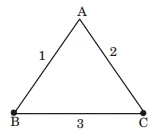
- Option : A
- Explanation :
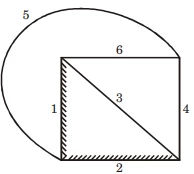 Here 3 can’t be taken because it will produce a
cycle so take 4.
This solution is 1 + 2 + 4 = 7
Here 3 can’t be taken because it will produce a
cycle so take 4.
This solution is 1 + 2 + 4 = 7


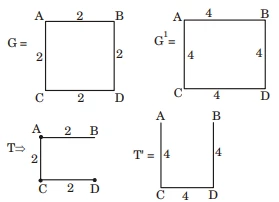 so both tree are different and. t' ≠ t2
so option D
is correct
so both tree are different and. t' ≠ t2
so option D
is correct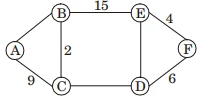
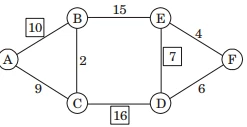 Total sum = 10 + 9 + 2 + 15 + 16 + 7 + 4 + 6 = 69
Total sum = 10 + 9 + 2 + 15 + 16 + 7 + 4 + 6 = 69