DT Q9
0. Consider the directed graph given below.
Which one of the following is TRUE?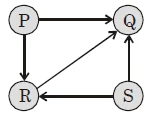
- Option : C
- Explanation : Topological ordering of a directed graph is a linear ordering of its vertices such that for every directed edge uv from vertex u to vertex v, u comes before v in the ordering. Topological ordering is possible iff graph has no directed cycles. (A) As the given graph doesn’t contain any directed cycles, it has at least one topological ordering. So option (A) is false (B) PQRS cannot be topological ordering because S should come before R in the ordering as there is a directed edge from S to R. SRQP cannot be topological ordering, because P should come before Q in the ordering as there is a directed edge from P to Q (C) PSRQ and SPRQ are topological orderings as both of then satisfy the above mentioned topological ordering conditions. (D) PSRQ is not the only one topological ordering as SPRQ is other possibility.


