Gate2019 cs Q22

0. Let G be an undirected complete graph on 𝑛 vertices, where n > 2. Then, the number of different Hamiltonian cycles in G is equal to

Answer
Comment
Array

Option : D
Explanation :
In a complete graph we can traverse the n vertices in any order and return to the starting vertex and form a Hamiltonian cycle. The number of such cycles will be n!

However, since circular rotations will have to ignored. Since for example K4 with vertices {1, 2, 3, 4}, the cycle 1-2-3-4 is same as 2-3-4-1 is same as 3-4-1-2 etc. we now get only (n – 1)! distinct Hamiltonian cycles. Further, the cycle 1-2-3-4 and 1-4-3-2 are also same (clockwise and anticlockwise).

So ignoring this orientation also we finally get 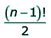distinct Hamiltonian cycles.

Forgot your password?

I agree with the Terms.