For the circuit shown for AB = 00, AB = 01, C, S values respectively are
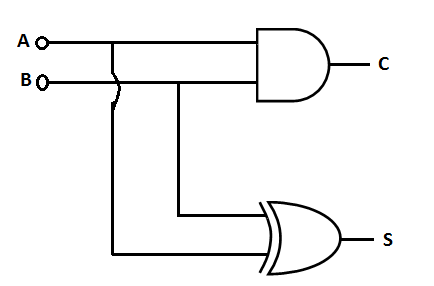
| A. | 0 , 0 and 0, 1 |
| B. | 0, 0 and 1, 0 |
| C. | 0, 1 and 0, 0 |
| D. | 1, 0 and 0, 0 |
|
Option: A Explanation : Click on Discuss to view users comments. Anilkumar said: (8:19am on Sunday 16th June 2013)
for c A=0,B=0 the gate will be AND according AND property 0 0 =0 similarly in the case S the gate will be NOR gate if input is 1 1 the output are 1 similarly remain output 0 1
|
What logic gate is represented by the circuit shown below?
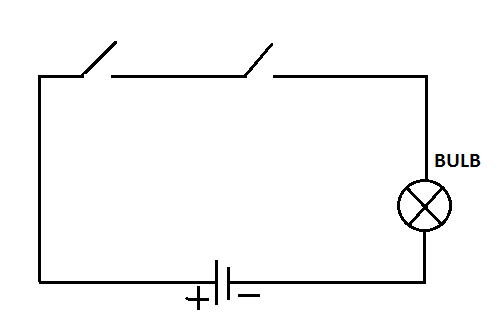
| A. | NAND |
| B. | NOR |
| C. | AND |
| D. | EQUIVALENCE |
|
Option: C Explanation : Click on Discuss to view users comments. vandna said: (10:30pm on Monday 9th September 2013)
in AND gate output is 1 if and only if both inputs are 1.if we look at this circuit,it will allow to pass the current only if both switches are closed.
aamir said: (2:31pm on Monday 31st October 2016)
The 2 switches (say A and B) are connected in series, so if one of them or both is/are open the current won't flow via bulb .
|
The circuit shown below is the
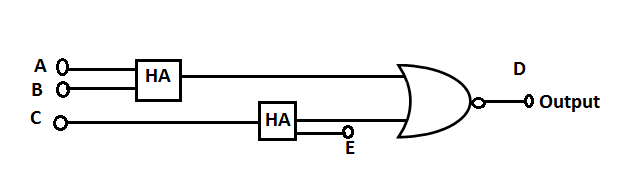
| A. | Full adder |
| B. | Full subtractor |
| C. | Parity checker |
| D. | None of these |
|
Option: A Explanation : Click on Discuss to view users comments. adit said: (2:06pm on Tuesday 14th May 2013)
But it's truth table with A,B,C,E as inputs dont looks like full adder
|
In the following gate network which gate is redundant
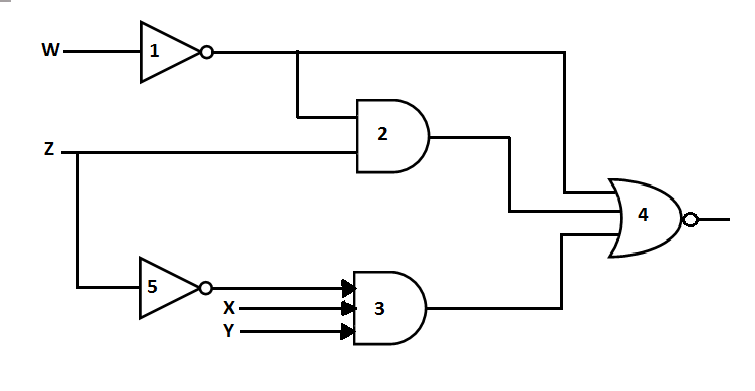
| A. | Gate no. 1 |
| B. | Gate no. 2 |
| C. | Gate no. 3 |
| D. | Gate no. 4 |
|
Option: B Explanation : Before Gate No. 4 being removed
Output, After Gate No. 4 being removed,
Output, Click on Discuss to view users comments. |
The combinational circuit given below is implemented with two NAND gates. To which of the following individual gates is its equivalent?

| A. | NOT |
| B. | OR |
| C. | AND |
| D. | XOR |
|
Option: C Explanation :
[ (a.b) '. (a.b) ' ] '= ((a.b)')' + ((a.b)')' Click on Discuss to view users comments. |