Answer = 0. 1 0 1 0…..
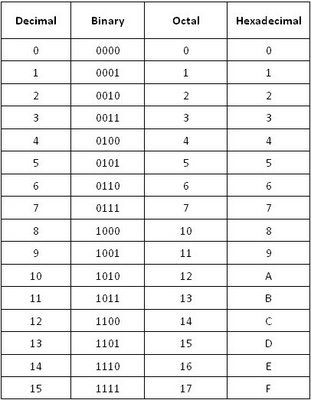
Octal Number System
-
Base or radix 8 number system.
-
1 octal digit is equivalent to 3 binary bits.
-
Octal numbers are 0 to7.
Conversion of octal to decimal
( base 8 to base 10)
Example: convert (635)8 to decimal
= (6 x 82) + (3 x 81) + (5 x 80)
= (6 x 64) + (3 x 8) + (5 x 1)
= 384 + 24 + 5
= (413)10
Conversion of decimal to octal ( base 10 to base 8)
Example: convert (178)10 to octal equivalent
178 / 8 = 22 remainder is 2
22 / 8 = 2 remainder is 6
2 / 8 = 0 remainder is 2
Answer = 2 6 2
Note: the answer is read from bottom to top as (262)8, the same as with the binary case.
Conversion of decimal fraction to octal fraction is carried out in the same manner as
decimal to binary except that now the multiplication is carried out by 8.
Example: convert (0.523)10 to octal equivalent up to 3 decimal places
0.523 x 8 = 4.184 ,its integer part is 4
0.184 x 8 = 1.472, its integer part is 1
0.472 x 8 = 3.776 , its integer part is 3
So the answer is (0.413..)8Conversion of decimal to binary (using octal)
When the numbers are large, conversion to binary would take a large number of division
by 2. It can be simplified by first converting the number to octal and then converting each
octal into its binary form:
Example: convert (177)10 to its binary equivalent using octal form
Step 1: convert it to the octal form first as shown above
This yields (2 6 1)8
Step 2: Now convert each octal code into its 3 bit binary form, thus 2 is replaced by 010,
6 is replaced by 110 and 1 is replaced by 001. The binary equivalent is
( 010 110 001)2
Example: convert (177.523)10 to its binary equivalent up to 6 decimal places using octal
form.
Step 1: convert 177 to its octal form first, to get (2 6 1)8 and then convert that to the
binary form as shown above, which is ( 010 110 001)2
Step 2: convert 0.523 to its octal form which is (0.413..)8
Step 3: convert this into the binary form, digit by digit. This yields (0.100 001 011…)
Step 4: Now put it all together
( 010 110 001 . 100 001 011…)2
Conversion of binary to decimal (using octal)
First convert the binary number into its octal form. Conversion of binary numbers to octal
simply requires grouping bits in the binary number into groups of three bits
•Groups are formed beginning with the Least Significant Bit and progressing to the MSB.
Start from right hand side and proceed to left. If the left most group contains only a
single digit or a double digit, add zeroes to make it 3 digits.
•Thus
11 100 1112
= 011 100 1112
= 3 4 78 And
1 100 010 101 010 010 0012
= 001 100 010 101 010 010 0012
= 14252218
Now it can be converted into the decimal form.