Calculus - Calculus MCQ

1. Home
2. Engineering Mathematics
3. Calculus
4. Calculus MCQ

6:  

The minimum value of | x2 _ 5x + 21 | is

A.	-5
B.	0
C.	-1
D.	-2
	Answer Report Discuss
	Option: B Explanation : Since value of a mod function cannot be less than zero, therefore f(x) = | x2 - 5x + 21 | is zero. Click on Discuss to view users comments. Write your comments here: Updating your Comments.. Updating your Comments..

7:  

 The value of the improper integral
 

A.	1/4
B.	0
C.	-1/4
D.	1
	Answer Report Discuss
	Option: C Explanation : Click on Discuss to view users comments. Write your comments here: Updating your Comments.. Updating your Comments..

8:  

Value of the definite integral

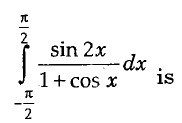
A.	-2ln2
B.	2
C.	0
D.	(ln2)2
	Answer Report Discuss
	Option: D Explanation : Click on Discuss to view users comments. Write your comments here: Updating your Comments.. Updating your Comments..

9:  

The function f(x) = 3x(x - 2) has a

A.	minimum at x = 1
B.	maximum at x = 1
C.	minimum at x = 2
D.	maximum at x = 2
	Answer Report Discuss
	Option: A Explanation : f(x) = 3x (x - 2) = 3x2 - 6x Differentiating, we get    Again diferentiating,  For maxima or minima, - f '(x) =0 ∴  6x-6=0  ⇒ x=1 As f '(x) =6 >0 then f(x) is minimum at x=1   Click on Discuss to view users comments. Write your comments here: Updating your Comments.. Updating your Comments..

10:  

What is the derivative of f(x) =  | x | at x = 0 

A.	1
B.	-1
C.	0
D.	Does not exist
	Answer Report Discuss
	Option: D Explanation : f(x) = |x| and f(x) = x for x > 0 ⇒f(x) = -x for x < 0 Hence from the graph it is clear that derivative doesn't exists for x=0 Click on Discuss to view users comments. Write your comments here: Updating your Comments.. Updating your Comments..

• «
• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• »