If 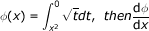
| A. | 2x2 |
| B. | √x |
| C. | 0 |
| D. | 1 |
|
Option: A Explanation :
Click on Discuss to view users comments. Sagnik Bhawal said: (1:56pm on Wednesday 5th August 2015)
while integrating how are the upper and lower limits getting changed? coz the integration doesn't result a negative sign. In absence of a negative sign how are the limits getting interchanged? i mean the answer should have been -2x^2 instead of 2x^2
ravi said: (5:48am on Saturday 5th December 2015)
it should be -2x^2
Waqar said: (1:57pm on Thursday 4th May 2017)
Dear, Its Answer Should be -2x square not 2x square. how can you exchange limits?
|
The function f(x) = x3 - 6x2 + 9x + 25 has
| A. | a maxima at x= 1 and a minima at x = 3 |
| B. | a maxima at x = 3 and a minima at x = 1 |
| C. | no maxima, but a minima at x = 1 |
| D. | a maxima at x = 1, but no minima |
|
Option: A Explanation :
f '(x) = 3(x2-4x+3) f ''(x)=6(x)-12 Click on Discuss to view users comments. abc said: (9:22am on Friday 5th April 2013)
how x=1 and x=3 arrive??
Akem said: (1:02pm on Tuesday 8th September 2015)
i taught maxima at x=3 because is positive and minima at x = 1 because it is negative
Jay Vyas said: (4:14pm on Friday 27th November 2015)
at X = 1 We got minimum value and at X= 3 we got maximum valueSo in my opinion option B is right
Samrah said: (2:38am on Wednesday 13th July 2016)
Take 1st derivative of the function and put it equal to 0 to find the value of "x".Now take 2nd derivative and put the 2 values of X previously found in equation to get a result respectively. If the final answer is ve so it is a Minima. If the answer is -ve it is a maxima.
|
The value of a = is
is
| A. | >0 |
| B. | 2 |
| C. | 0 - 1 + 100 - 10 + 1 |
| D. | undefined |
|
Option: A Explanation :
Click on Discuss to view users comments. kiran said: (2:23am on Friday 2nd December 2016)
how cos5p=-1
|
The interval in which the Lagrange's theorem is applicable for the function f(x) = 1/x is
| A. | [-3, 3] |
| B. | [-2, 2] |
| C. | [2, 3] |
| D. | [-1, 1] |
|
Option: C Explanation : Since f(x) = (1/x) is not continuous in [- 3, 3] [- 4, 2] or [- 1, 1], The point of discontinuity is '0'. Only in [2, 3] the function is continuous, and differentiable hence mean value theorem is applicable in [2, 3]. Click on Discuss to view users comments. |
If f(x) = | x | , then for interval [-1, 1] ,f(x)
| A. | satisied all the conditions of Rolle's Theorem |
| B. | satisfied all the conditions of Mean Value Theorem |
| C. | does not satisied the -conditions of Mean Value Theorem |
| D. | None of these |
|
Option: C Explanation : Since f(x) = |x| is continuous in [-1, 1] but it is not differentiable at x = 0 ε (-1, 1) Click on Discuss to view users comments. |