| A. | Dijkstra's algorithm |
| B. | Floyd's algorithm |
| C. | Prim's algorithm |
| D. | Warshall's algorithm |
|
Option: B Explanation : Dijkstra's algorithm solves single source shortest path problem. Warshall's algorithm finds transitive closure of a given graph. Prim's algorithm constructs a minimum cost spanning tree for a given weighted graph. Click on Discuss to view users comments. |
| A. |
O(m)
|
| B. | O(n) |
| C. | O(m+n) |
| D. | O(log(m) + log(n)) |
|
Option: C Explanation : Click on Discuss to view users comments. |
| A. | makes debugging difficult. |
| B. | increases the running time of programs |
| C. |
increases memory requirement of programs
|
| D. | results in the compiler generating longer machine code |
|
Option: A Explanation : Click on Discuss to view users comments. |
Which of the following algorithm design technique is used in the quick sort algorithm?
| A. |
Dynamic programming
|
| B. |
Backtracking
|
| C. | Divide and conquer |
| D. | Greedy method |
|
Option: C Explanation : Click on Discuss to view users comments. |
Which one of the following statements is false?
| A. |
Optimal binary search tree construction can be performed efficiently using dynamic programmmg.
|
| B. |
Breadth-first search cannot be used to find connected components of a graph.
|
| C. |
Given the prefix and postfix walks of a binary tree, the binary tree cannot be uniquely reconstructed.
|
| D. | Both (b) and (c) |
|
Option: D Explanation :
Here option (B) is also false because BFS and DFS both algorithm are used to find connected component. For example: In BFS, a search that begins at some particular vertex 'v' will find the entire connected component containing v (and no more) before returning. To find all the connected components of a graph, loop through its vertices, starting a new breadth first search whenever the loop reaches a vertex that has not already been included in a previously found connected component. For example:If we do the breadth first traversal of the above graph and print the visited node as the output, it will print the following output. “A B C D E F”. The BFS visits the nodes level by level, so it will start with level 0 which is the root node, and then it moves to the next levels which are B, C and D, then the last levels which are E and F.
In BFS, a search that begins at some particular vertex v will find the entire connected component containing v (and no more) before returning. To find all the connected components of a graph, loop through its vertices, starting a new breadth first search whenever the loop reaches a vertex that has not already been included in a previously found connected component. so ans is both 'A' and 'C'
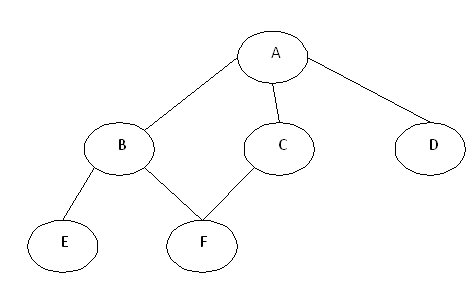 Click on Discuss to view users comments. |